7. Quelles sont les limites des codes détecteurs et correcteurs d’erreurs ?
Nous avons vu dans le cas du code par répétition que toutes les anomalies ne sont pas forcément détectées ou corrigées correctement. Qu’en est-il pour le code de double parité ? Les exemples que nous donnons dans cette vidéo illustrent les différents aspects de la nature imparfaite des codes en s’appuyant sur l’exemple du code de double parité.
Avez-vous retenu ?
- Au minimum, si on utilise le code de double parité, quel est le nombre d’erreurs dans un message si on détecte des erreurs sans pouvoir les corriger ?
- Pour le code de double parité, existe-t-il des cas où des erreurs sont corrigées de façon inexacte ? Si oui, donner un exemple.
- Existe-t-il des cas où le code de double parité ne détecte pas des erreurs existantes ? Si oui, donner un exemple.
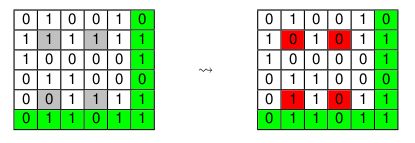
- Ce cas peut se produire à partir de deux erreurs : plusieurs corrections ont la même probabilité, on ne peut pas choisir entre elles (voir des exemples dans la vidéo). Voici deux exemples supplémentaires sur le schéma ci-dessous : le message émis est à gauche, et sur les deux messages reçus à droite, on note en rouge les bits erronés et en bleu le résultat de la détection. Le premier message reçu comporte deux erreurs et le deuxième en comporte quatre. À noter, sur l’exemple le plus à droite, que les deux façons de rétablir la règle de parité en modifiant le moins de bits possibles (c’est-à-dire les corrections éventuellement proposées), sont toutes les deux inexactes.
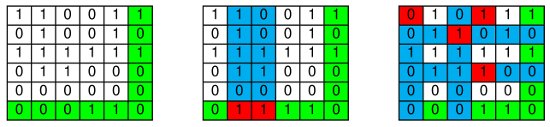
- Oui, ce cas peut se produire à partir de trois erreurs (voir un exemple dans la vidéo). Voici deux exemples supplémentaires sur le schéma ci-dessous : le message émis est à gauche, et sur les deux messages reçus à droite, on note en rouge les bits erronés et en bleu le résultat de la détection. Le premier message reçu comporte trois erreurs et le deuxième en comporte sept.
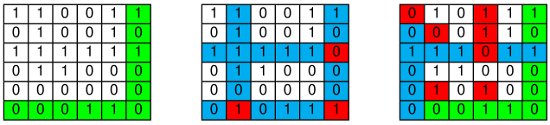
- Oui, ce cas peut se produire à partir de quatre erreurs (voir un exemple dans la vidéo). Voici deux exemples supplémentaires sur le schéma ci-dessous : le message émis est à gauche, et sur les deux messages reçus à droite, on note en rouge les bits erronés et en bleu le résultat de la détection. Le premier message reçu comporte quatre erreurs et le deuxième en comporte huit.
Notions importantes :
- Détecter une anomalie et ne pas savoir la corriger (correction ambigue)
- Détecter une anomalie et effectuer une correction inexacte
- Ne pas détecter une anomalie
Comment la correction d’un message erroné se déroule-t-elle lorsque deux ou plusieurs mots de code ont autant de chance d’être le message émis ?
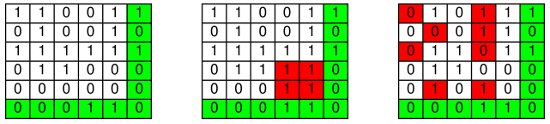
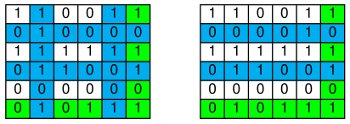
C’est ce qui se passe dans les deux exemples ci-dessous :
- à gauche, deux lignes et deux colonnes ne respectent pas la règle de parité. Il y a deux façons différentes de corriger en modifiant le moins de bits possibles : en agissant sur les bits qui se trouvent ou bien en ligne 2 colonne 2 et en ligne 4 colonne 5, ou bien en ligne 2 colonne 5 et en ligne 4 colonne 2. Dans les deux cas, deux bits sont corrigés, et les deux mots de code obtenus ont autant de chance l’un que l’autre d’être le message émis.
- à droite, deux lignes ne respectent pas la règle de parité, et toutes les colonnes la respectent. Il y a six façons différentes de corriger en modifiant le moins de bits possibles : en agissant sur les bits en lignes 2 et 4 de n’importe quelle colonne. Dans les six cas, deux bits sont corrigés, et les six mots de code obtenus ont autant de chance les uns que les autres d’être le message émis.
Lorsqu’il y a une ambigüité sur le mot de code à choisir pour la correction, par convention, le message reçu n’est pas du tout corrigé. Parfois, une “erreur non corrigeable” est indiquée, parfois rien du tout. La raison de ce choix est de ne pas risquer d’introduire des erreurs supplémentaires dans le message reçu.
Question d’approfondissement
À quelle situation de la vidéo numéro 4 se rattachent :
- Le message comportant 4 erreurs étudié dans la vidéo numéro 7 ?
- Le message comportant 3 erreurs étudié dans la vidéo numéro 7 ?
- Le message comportant 4 erreurs correspond à la situation où l’ensemble des erreurs pendant la transmission a transformé le message émis en un mot de code différent.
- Le message comportant 4 erreurs correspond à la situation où l’ensemble des erreurs pendant la transmission a donné un message reçu plus éloigné du message émis que d’un autre mot de code.
