Introduction

La machine enigma est une machine de chiffremnt créée par Arthur Scherbius, elle était principalement utilisée par l’Allemagne Nazi durant la seconde guerre mondiale. La premiere personne à avoir “casser” la machine fut Marian Rejewski un mathématicien et cryptanalyste polonais, puis plus tard Alan Turing a créé “La bombe” qui a permis d’accelerer grandement le processus de dechiffrement, ce qui a fait une grande différence dans la victoire des alliés durant la guerre.

Fonctionnement

Chiffrement:

Notre version de la machine se représente sous la forme d'une roue:

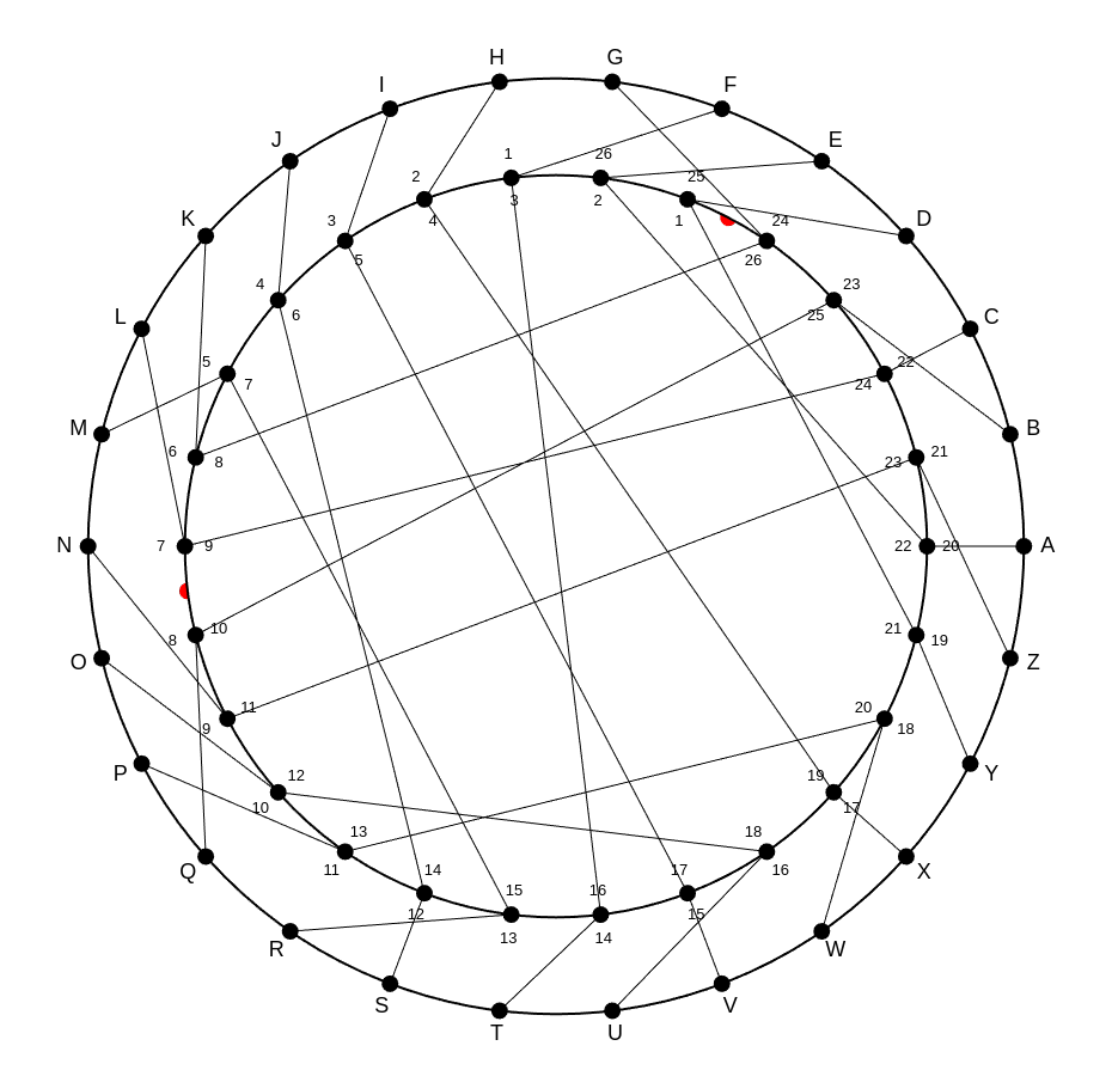
Version simple: On ne prend pas en compte les encoches rouges dans cette version, le seul rotor a tourné est le rotor intérieur.

Première étape: On choisi une rotation initiale pour le rotor
Deuxième étape: On lit la lettre correspondante en suivant les traits, une fois la lettre lu, on tourne le rotor d'un cran dans le sens inverse des aiguilles d'une montre. On répète l'opération jusqu'à finir de chiffrer le message.

Version 2 rotor: Les deux rotors peuvent tourner

Première étape: On choisi une rotation initiale pour les 2 rotors
Deuxième étape: On lit la lettre correspondante en suivant les traits, une fois la lettre lu, on tourne le rotor d'un cran dans le sens inverse des aiguilles d'une montre. si les deux encoches rouge sont alignées, alors on tourne aussi d'un cran le deuxième rotor dans le même sens que le premier. Les deux encoches sont donc encore alignées mais on ne re-tourne pas le deuxième rotor directement, on continue les étapes seulement avec le premier rotor. On répète l'opération jusqu'à finir de chiffrer le message.

Exemple

En utilisant la roue disponible plus haut, le message "Bonjour" avec une rotation initiale de 22 et 20 se chiffre en "QCGXHBH".

Déchiffrement

Avec les clésPour déchiffrer un message lorsqu'on a toutes les infos d'orientation et de connexions, on applique la même méthode que pour le chiffrement.

Sans l'orientationOn teste toute les possibilités d'orientation en appliquant la même méthode que le chiffrement. Si on a le début de la solution cela enlève des cas possibles.