Après avoir expliqué ce que sont les codes détecteurs et correcteurs d’erreurs et pourquoi ils sont indispensables aux communications numériques, nous présentons un premier exemple de code détecteur et correcteur d’erreurs. C’est celui qui est utilisé dans l’activité pour la classe. Il repose sur des notions mathématiques très simples (lignes et colonnes d’un tableau, nombres pairs et impairs).

• Texte seul :
• Diapositives seules :

Avez-vous retenu ?

1. Calculer le bit de parité permettant de compléter la ligne 0 1 1 0 0 selon le principe du code de double parité.
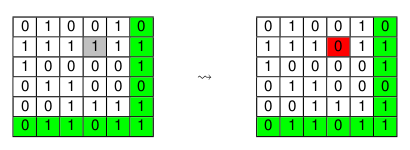
2. Trouver et corriger l’erreur dans le message ci-dessous, qui a été traité auparavant en utilisant le code de double parité :
   

Notion importante :

Fonctionnement du code de double parité

Pourquoi, dans ce chapitre, le message est-il représenté sous la forme d’un carré de bits et non d’une séquence de bits comme dans le chapitre précédent ?

En réalité, l’ordinateur travaille bien sur des séquences de bits, et il connaît la correspondance entre chaque bit de parité et les cinq bits dont il dépend.

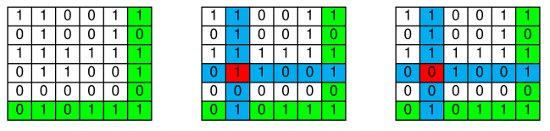
Sur le schéma ci-dessous, dans la partie du haut, les couleurs montrent comment construire la représentation sous forme d’un carré de bits à partir d’une séquence de bits. Ensuite, une fois le code correcteur appliqué, la partie du bas du schéma explique comment obtenir la séquence de bits calculée par l’ordinateur, en ajoutant les bits de parité à la fin de la séquence initiale.

Ainsi, plutôt que de devoir expliquer comment passer de la séquence de bits de la première ligne à la séquence de bits de la dernière ligne, il est beaucoup plus simple, comme nous l’avons fait dans la vidéo, de présenter les calculs à l’aide des représentations sous forme de carrés de bits qui se trouvent au milieu.

Quel est le rôle du 36e bit ?

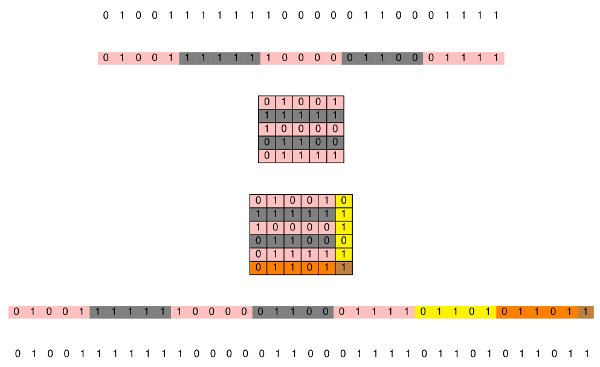
Ce bit, situé à l’intersection de la ligne et de la colonne ajoutées, est un bit de parité, calculé à partir de la colonne ou de la ligne des bits de parité. En effet, ces derniers sont des bits transmis comme les autres, et donc potentiellement sujets à des erreurs. Ce 36e bit sert uniquement à repérer une erreur dans la transmission des bits de parité. Il est remarquable qu’on puisse le calculer indifféremment à partir de la colonne ou de la ligne des bits de parité. Cela vient du fait qu’il ne dépend que de la parité du nombre de 1 dans l’ensemble du carré 5x5 initial. (En termes techniques, on dit que l’addition modulo 2 étant commutative et associative, le résultat obtenu est le même en sommant d’abord sur les lignes, puis sur la colonne obtenue, ou bien le contraire.)

Sur le schéma ci-dessous, le message émis est à gauche, et le message reçu à droite : une erreur se produit parmi les bits de parité, et le code de double parité permet de la détecter et de la corriger. À noter que la détection/correction marche encore si c’est le 36e bit lui-même qui est modifié au cours de la transmission.

Et si les données initiales ne comportent pas exactement 25 bits pour en faire un carré de 5x5 ?

En premier lieu, nous verrons dans le prochain chapitre que les données initiales sont découpées en blocs d’une longueur fixe et adaptée pour chaque code. Mais quoiqu’il en soit, le code de double parité est heureusement assez flexible et s’adapte facilement à d’autres situations. Les schémas ci-dessous montrent quelques variantes de la version présentée dans la vidéo.

• Un message initial de 9 bits, qui donne un carré de 3x3
  
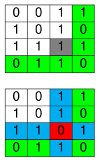
• Un message initial de 35 bits, qui donne un rectangle de 5x7
  
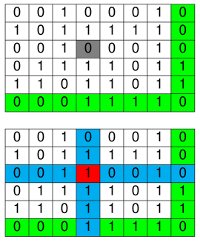
• Un message initial de 23 bits, auquel sont ajoutés 2 bits “de remplissage” quelconques (par exemple des zéros) pour se ramener à un carré de 5x5
  
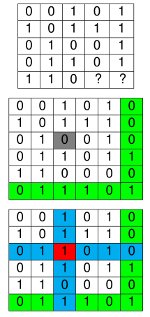
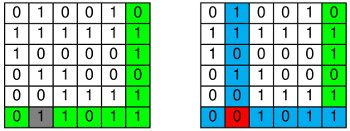
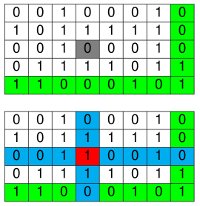
• Un message initial de 28 bits, qui donne (par exemple) un rectangle de 4x7

Dans ce dernier cas, le code de double parité fonctionne encore, comme on le voit sur le schéma. Cependant, il ne faut pas confondre les rôles des 0 et des 1. En effet, sur les colonnes, après ajout des bits de parité, les deux chiffres ne jouent pas un rôle symétrique : s’il y a un nombre pair de 1, alors il y a un nombre impair de zéros. Cette subtilité se présente chaque fois que le nombre de lignes (ou de colonnes) avant ajout des bits de parité est pair. L’introduction du code de double parité avec une situation initiale ne présentant pas ce risque de confusion nous a paru préférable.

Question d’approfondissement

Dans la vidéo du chapitre 2, les mots “codage”, “décodage” et “bits de contrôle”, introduits dans le chapitre 1, n’ont volontairement pas été utilisés. À quoi correspondent-ils dans le cas du code de double parité ?

Remarque

Les noms des personnages d’Alice et Bob qui apparaissent dans cette vidéo (illustrations non contractuelles) sont traditionnellement utilisés par les informaticiens pour nommer l’expéditeur et le destinataire d’un message, en particulier en cryptologie, c’est-à-dire en ce qui concerne la sécurité des échanges. Leur principale qualité semble bien être qu’ils commencent respectivement par A et B…